Mandelbrotmengden
Mandelbrotmengden er en fraktal, oppkalt etter den franske matematikeren Benoît Mandelbrot.
Definisjon[rediger | rediger kilde]
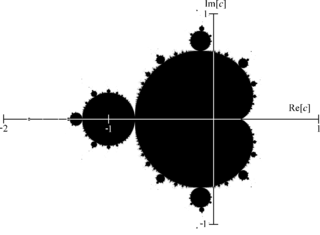
La c være et komplekst tall. Definer en følge av komplekse tall z0, z1, z2, ... ved
Mandelbrotmengden , består av alle komplekse tall c slik at denne tallfølgen er begrenset, det vil si at den ikke divergerer mot uendelig. Figuren til høyre viser mandelbrotmengden tegnet i det komplekse planet.
Egenskaper[rediger | rediger kilde]
Mandelbrotmengden har mange interessante egenskaper. Hvis man zoomer inn langs randen av mandelbrotmengden, vil man kunne finne små kopier, kalt satellitter, av mandelbrotmengden selv. Hvis man tar et hvilket som helst utsnitt av det komplekse planet som både inneholder punkter i og punkter utenfor , vil det innholde uendelig mange satellitter.
Bildegalleri[rediger | rediger kilde]
Denne bildesekvensen er en zoomreise til et bestemt punkt c i det komplekse planet. Hvert bilde er et utsnitt av det foregående. Det siste bildet er en forstørrelse av det første på omtrent 60 milliarder. De svarte punktene er selve mandelbrotmengden. De fargelagte punktene er punkter utenfor mandelbrotmengden, og fargen er bestemt ut fra hvor raskt følgen definert ovenfor divergerer.
-
Start
-
Utsnitt 1
-
Utsnitt 2
-
Utsnitt 3
-
Utsnitt 4
-
Utsnitt 5
-
Utsnitt 6
-
Utsnitt 7
-
Utsnitt 8
-
Utsnitt 9
-
Utsnitt 10
-
Utsnitt 11
-
Utsnitt 12
-
Utsnitt 13
-
Utsnitt 14


















