Kumulativ fordelingsfunksjon

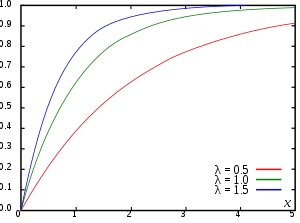
Den kumulative fordelingsfunksjonen beskriver en sannsynlighetsfordeling for en stokastisk variabel innenfor matematisk statistikk. For en stokastisk variabel X, med sannsynlighetsfunksjonen P(x), defineres den kumulative fordelingsfunksjonen F_X(x) som:

$F_X(x) = P(X\leq x)$

Den kumulative fordelingsfunksjonen er monotont stigende og har, blant annet, alltid følgende egenskaper:

• $\lim_{x \to -\infty} F(x) = 0,$

• $\lim_{x \to \infty} F(x) = 1,$

• $0 \le F(x) \le 1.$

For en diskret stokastisk variabel som kan anta verdiene x₁, x₂... er F diskontinuerlig i punktene x_i og har konstant verdi mellom dem, det vil si at den har et trappetrinnlignende utseende.

For en kontinuerlig stokastisk variabel er F lik

$F(x) = \int_{-\infty}^x f(t) dt$

der f(t) er tetthetsfunksjonen (eller frekvensfunksjonen) for variabelens fordeling.

Sannsynligheten for at en stokastisk variabel skal anta verdier større enn a og mindre eller lika b kan finnes ved:

$P(a < X \le b) = F(b) - F(a)$

Tabell over verdiene hos den kumulative normalfordelingsfunksjonen ligger her. Andre fordelinger har andre tabeller.