Topologisk sortering
Topologisk sortering er arbeidet med å sortere nodene i en graf slik at naboer listes i rett innebyrdes orden. Det forutsettes at to noder bare har en rettet kant seg imellom, og at grafen er asyklisk.
Problemstillingen opptrer for eksempel i prosjektplanlegging, og beregninger i regneark, der avhengigheter gjør at arbeid må utføres i rett rekkefølge. Grafens noder er da henholdsvis aktivitet i prosjektet eller en celleberegning.
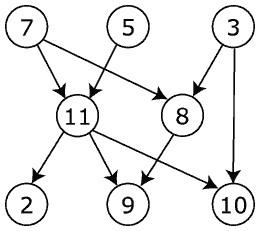
Den avbildede rettede asykliske graf (t.h.) har flere mulige topologiske sorteringer:
- 7,5,3,11,8,2,9,10
- 7,5,11,2,3,10,8,9
- 3,7,8,5,11,10,9,2
En vanlig algoritme for å finne en av løsningene, er da å
- Initielt
- finne ut hvilke noder som er naboer (a har nabo b kun hvis det fins en rettet kant fra a til b)
- regn ut inn-graden g(n) til hver node n i grafen.
- Noder med g(n) lik 0 legges i mengden STARTPUNKT
- I en løkke vil man, sålenge det finnes noder i STARTPUNKT
- velge ut en node i fra mengden STARTPUNKT
- skriv ut i
- fjern i fra STARTPUNKT
- for hver av i's naboer, j
- reduser g(j) med 1
- hvis g(j) har blitt 0, legg j til mengden STARTPUNKT
- Utskriften inneholder den sorterte liste.
Hvis grafen er syklisk avsløres det med at g(j) har antatt negative verdier.
