Pulsbreddemodulasjon
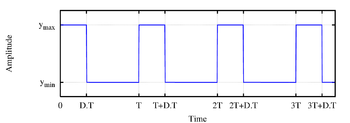
Pulsbreddemodulasjon eller pulsbreddemodulering (PBM eller engelsk Pulse-Width Modulation, PWM) er styring av et firkantpulstog på en slik måte at de aktive pulslengdene endres, mens periodetiden (og derfor grunnfrekvensen) er konstant. Forholdet mellom den aktive tiden (D.T i illustrasjonen) og periodetiden T blir D.T/T og kalles pulstogets arbeidssyklus, også kjent som duty cycle (på engelsk). Den aktive pulslengden D.T kan ligge mellom 0 og 100 % av periodetiden, altså mellom 0 og T.
Ved integrering av pulstoget oppstår en spenning som tilsvarer pulslengdens prosentandel av den aktive spenningen – . Dette kan måles som effektiv-verdien av spenningen, som er et resultat av pulsbredden. Det er oftest hovedformålet med prosessen å styre en spenning slik. For overføring av styrespenningen, nyttesignalet, kan en bruke en kanal som ikke kan overføre så lave frekvenser, for eksempel likestrøm.
Pulsbreddemodulasjon brukes i stor grad til å regulere hastighet på likestrømsmotorer, lysstyring og til andre reguleringsformål. Fordelene med denne type regulering er at det oppstår veldig lite tap i systemet, sammenlignet med for eksempel serieregulatorsystemer.
I modulasjonsterminologi styrer nyttesignalet pulsbredden, og bæresignalet er en likespenning (lik – ). Demodulasjon gjøres ved hjelp av integrering, som her gjøres ved lavpassfiltrering. Se pol.
Den demodulerte spenningen kan ikke inneholde frekvenser som er høyere enn halve signalfrekvensen 1/T, noe som følger av samplingsteoremet.
Matematisk utledning av demodulasjonen[rediger | rediger kilde]
Det modulerte signalet kan generelt uttrykkes som Demodulasjonen kan beregnes ved midlet integrasjon av signalet over en periode:
Spenningsverdiene av er
for tiden og
for tiden , og integrasjonen gir oss:
Dette uttrykket kan forenkles der og vi får .
Av dette ser en at middelvedien av utsignalet () er proporsjonal med duty cycle D.T.

En enkel måte å generere et PBM-signal på er ved hjelp av en sagtanngenerator og en komparator. Når nyttesignalet, her gitt ved den grønne sinuskurven, er større enn sagtannsignalet (blå) settes utgangssignalet (magenta) «høyt», ellers settes det «lavt», se figur 2.
En annen, og kanskje den mest brukte, metoden idag er ved hjelp av mikroprosessorer som kan være spesialdesignet til dette formålet.











