Skjæringssetningen

Illustration av skjæringssetningens betydning.

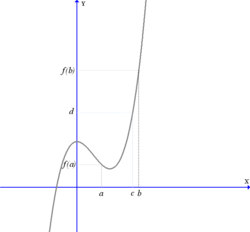
Skjæringssetningen er en matematisk setning som forteller at en reell kontinuerlig funksjon $f$ definert på et lukket intervall fra $a$ til $b$ vil treffe alle verdier mellom $f(a)$ og $f(b)$.

Setningen er viktig, da den kan benyttes som argument for eksistensen av en rekke reelle tall. For eksempel kan eksistensen av ${\sqrt {2}}$ påvises ved betraktning av funksjonen $f\colon [0,\infty )\to \mathbb {R}$ gitt ved $f(x)=x^{2}-2$. Funksjonen gir ut både negative og positive verdier, og må derfor ha et nullpunkt. Punktet hvor funksjonen blir $0$ kalles da ${\sqrt {2}}$.

Formell formulering

La $f\colon [a,b]\to \mathbb {R}$ være en kontinuerlig funksjon og $d$ være et reelt tall mellom $f(a)$ og $f(b)$. Da eksisterer et tall $c\in (a,b)$ slik at $f(c)=d$.

Denne artikkelen er en spire. Du kan hjelpe Wikipedia ved å utvide den.