Lagrange-multiplikator
Bruk av Lagrange-multiplikator kjennetegner en metode for bestemmelse av ekstremalverdier av en funksjon med flere variabler når disse må oppfylle en eller flere bibetingelser. Den er oppkalt etter den franske matematiker Joseph Louis Lagrange som utviklet den i forbindelse med sine første arbeider innen variasjonsregningen.
Ekstremalisering med bibetingelser[rediger | rediger kilde]
For at en kontinuerlig funksjon
av to variable x og y skal ha en maksimal eller minimal verdi, må
være null i ekstremalpunktet.
Men noen ganger kan det eksistere et krav om at de to variable må oppfylle en bibetingelse.
Den kan man alltid skrive på formen
hvor c er en konstant.
Nå er differensialet av denne funksjonen
slik at dx og dy ikke lenger er uavhengige av hverandre.
Forholdet mellom dem er gitt som dy/dx = - gx/gy. Men fra kravet at df = 0 finner man på samme måte at dy/dx = - fx/fy slik at de deriverte må oppfylle relasjonen gx/gy = fx/fy i ekstremalpunktet. Det kan man få til ved at fx = - λgx og fy = - λgy hvor λ er vilkårlig. Men hvis nå λ er konstant, ser man at disse to kravene blir begge oppfylt ved å bestemme ekstremalverdien av funksjonen
hvor nå x og y varierer fritt. Det gir nemlig betingelsene ∂ f*/∂ x = ∂ f/∂ x + λ∂ g/∂ x = 0 og tilsvarende for den deriverte med hensyn på y. Denne konstanten λ er en Lagrange-multiplikator.
Skal man bestemme ekstremalverdiene for en funksjon f(x,y,...) av mer enn to variable, kan man gå frem på samme måte. Man kan da også ha flere bibetingelser gi (x,y,...) = ci som kan tas hensyn til ved å innføre en Lagrange-multiplikator λi for hver av dem. Problemet løses i dette tilfellet ved å finne minima eller maksima av funksjonen
hvor de variable nå kan betraktes som uavhengige av hverandre.
Eksempel[rediger | rediger kilde]

Et rektangel skal innskrives i en ellipse med akser a og b, det vil si beskrevet ved ligningen
Man skal nå bestemme sidene i rektangelet når dets areal A er størst mulig. Ut fra symmetrigrunner må disse være parallelle med aksen til ellipsen slik at A = 4xy. Denne funksjonen av x og y skal maksimaliseres samtidig ved at ligningen til ellipsen er oppfylt. Man må da finne maksimum av den modifiserte funksjonen
Ekstremalpunktet er dermed gitt ved ligningene ∂ A*/∂ x = 4y + 2λx/a2 = 0 og ∂ A*/∂ y = 4x + 2λy/b2 = 0. Multipliseres den første med x, den andre med y og legger man så sammen de to resulterende ligningene, finner man at 8xy + 2λ = 0. Derfor må man ha at λ = - 4xy. Innsetter man nå dette resultatet i f.eks. den første ligningen, tar den formen
Her er y = 0 en løsning, men den gir en minimalverdi for arealet, nemlig A = 0. Den andre løsningen x = a/√2 som medfører at y = b/√2, gir derimot verdien A = 2ab som er den søkte maksimalverdien.
Geometrisk utledning[rediger | rediger kilde]
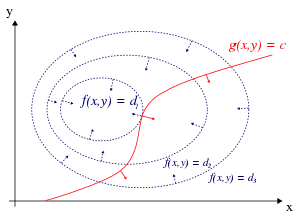
Bibetingelsen g(x,y) = c definerer en kurve i (x,y) - planet som vist i figuren. Den vil vanligvis skjære gjennom koter for funksjonen f(x,y). I figuren er disse lukkede kurver hvor funksjonen antar en konstant verdi. At den skjærer gjennom en kote i et punkt, betyr at der forandrer funksjonen seg slik at den ikke kan ha noe ekstremalpunkt der.
Men hvis det finnes et punkt hvor kurven g(x,y) = c tangerer en kote, vil dette punktet være et ekstremalpunkt. Tangenten til kurven vil her være parallell med tangenten til koten. Nå er gradienten ∇g til kurven en vektor som står vinkelrett på dens tangent i hvert punkt. På samme måte står gradienten ∇f vinkelrett på kotene til funksjonen f(x,y) som vist med pilene i figuren. I et ekstremalpunkt vil derfor normalene til de to kurvene være parallelle, det vil si at vi har en relasjon ∇f = -λ ∇g. Hvis nå λ er en konstant, vil derfor betingelsen for et ekstremalpunkt være
Komponentene av denne ene vektorligningen gir det samme resultatet som fra de enkelte ligningene funnet tidligere. Om dette er et maksimal- eller minimalpunkt, kan finnes ved å beregne de andrederiverte av funksjonen eller ved direkte utregning av funksjonsverdier.
Litteratur[rediger | rediger kilde]
- J. E. Mathews and R. L. Walker, Mathematical Methods of Physics, W.A. Benjamin, Inc., New York (1964).
- L. E. Elsgolc, Calculus of Variations, Addison-Wesley Publishing Company, New York (1961).
Eksterne lenker[rediger | rediger kilde]
- MathWorld: Lagrange Multiplier










