Plancks strålingslov
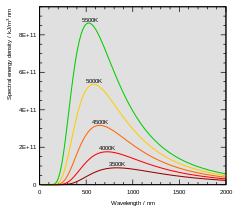
Plancks strålingslov ble funnet av den tyske fysiker Max Planck i slutten av året 1900. Det er en matematisk formel for den spektrale energitettheten eller intensiteten til varmestrålingen som avgis fra et svart legeme med en viss temperatur. Resultatet ble funnet etter flere års forskning basert på bruk av Maxwells ligninger for de elektromagnetiske bølgene som utgjør strålingen, kombinert med termodynamikkens lover. Man antok at denne var i termisk likevekt med atomene i veggene som omsluttet strålingen. Man hadde på den tiden omtrent ingen kjennskap til atomenes egenskaper. Men allerede fra etableringen av Kirchhoffs strålingslov i 1860 var det klart at egenskapene til selve strålingen var uavhengig av materialet i veggene eller atomene de inneholdt.
Avgjørende for denne oppdagelsen var nye, mer presise målinger som viste at tidligere forslag til strålingslover ikke var riktige. Planck benyttet disse eksperimentelle resultatene til først å gjette seg frem til en riktig formel som han senere ga en teoretisk utledning. Det var da nødvendig å anta at energien som kunne absorberes og emitteres av atomene som var koblet til strålingen, ikke kunne overføres kontinuerlig som i klassisk fysikk. Derimot måtte det skje i små, diskrete pakker som ble kalt energikvant. Et slikt kvant er karakterisert ved en ny naturkonstant h som senere er blitt kalt for Plancks konstant. Planck holdt imidlertid fast ved at selve strålingen skulle betraktes som kontinuerlig og beskrives ved de vanlige Maxwell-ligningene. Dette fastholdt han frem til moderne kvantemekanikk ble etablert rundt 1925 og var ikke til hinder for at han mottok Nobel-prisen i fysikk i 1918.
Albert Einstein var på den tiden den som tok Plancks resultat opp med størst interesse. Ved bruk av termodynamikk og statistisk mekanikk viste han at selve strålingen måtte antas å ha en diskrete natur, bestående av energikvant med energi E = hν for en bølge med frekvens ν. Dette kunne forklare egenskaper ved den fotoelektriske effekten, en forklaring som i 1921 ga Einstein Nobel-prisen i fysikk. En full forståelse av varmestrålingen kom likevel ikke før i 1926 med utviklingen av kvantefeltteori. Dette skyldes i mye større grad Einsteins innsats enn hva Planck selv hadde bidratt med, men likevel er det Max Planck og hans strålingsformel som representerer begynnelsen av moderne fysikk ved innføringen av kvantebegrepet.

Plancks formel[rediger | rediger kilde]
Den totale energien U(T) til den sorte strålingen i et volum V ved temperatur T er gitt ved energitettheten u(T) = U/V. Denne tettheten får bidrag fra forskjellige frekvenser ν av den elektromagnetiske strålingen den består av. Denne avhengigheten beskrives ved den spektrale energitettheten uν(T) slik at Vuνdν er den totale energien fra bølger i frekvensintervallet mellom ν og dν. Planck viste at denne tettheten gitt ved formelen
var i overensstemmelse med alle måleresultat og observasjoner. Her er kB Boltzmanns konstant og h den nye konstanten han hadde vært nødt til å innføre. Den oppfylte også det generelle kravet utledet tidligere av Wilhelm Wien at den måtte være ν3 multiplisert med en funksjon av ν/T som ligger bak Wiens forskyvningslov. Eksperimentelt har den fått den mest nøyaktige bekreftelse fra målingene av den spektrale intensiteten til den kosmiske bakgrunnsstrålingen gjennomført siden 1990.
For høye frekvenser som oppfyller hν > kBT, går dette uttrykket over i
som er Wiens strålingslov. I den motsatte grensen hν < kBT kan man benytte at ex ≈ 1 + x når x < 1. Det gir at
som er Rayleigh-Jeans' strålingslov. Det var akkurat denne lineære økningen med temperaturen som var påvist i målingene og som var den utløsende faktor for Planck til å prøve å finne en ny strålingsformel.
Stefan-Boltzmanns konstant[rediger | rediger kilde]
Den fulle energitettheten u(T) finnes ved å integrere over alle frekvenser ν fra null til uendelig. Ved å skifte integrasjonsvariabel til x = hν/kBT, er den da gitt som
- .
Integralet her har verdien π 4/15 slik at resultatet kan skrives som u = aT4. Da den utstrålte fluksen fra et sort legeme er Φ = (c/4)u, kan denne skrives som Φ = σT4 som er Stefan-Boltzmanns lov. Her inngår deres konstant σ = ca/4 som dermed blir
Verdien på denne var godt kjent på Plancks tid, og han benyttet den til å bestemme verdien til sin egen, nye konstant h.
Wiens forskyvningslov[rediger | rediger kilde]

Den spektrale energifordelingen til Planck har et maksimum som varierer med temperaturen. Historisk er det vanlig å beregne dette fra den sprektrale fordelingen uλ(T) med hensyn på bølglengden λ = c/ν. Denne defineres ved uλdλ = uνdν som gir
Bølgelengden ved maksimum av denne funksjonen finnes nå fra betingelsen ∂uλ/∂λ = 0. Ved å innføre x = hc/λkBT i stedet for λ som variabel, gir nå derivasjonen ligningen
Det betyr at x/5 = 1 - e -x som må løses numerisk. Man finner da at xm = 4,96511... ved maksimum. Den tilsvarende bølgelengden oppfyller dermed
Desto høyere temperaturen blir, desto mindre blir derfor bølgelengden for den maksimale intensiteten. Dette er Wiens forskyvningslov og stemte godt med eksperiment. Lummer og Pringsheim fant i 1900 at konstanten på høyre side hadde verdien 2940 μm⋅K, i meget god overensstemmelse med dagens verdi.[1]
Solen har en overflatetemperatur på ca. 5780 K som gir λm = 530 nm som tilsvarer synlig lys. Jorden med en overflatetemperatur på ca. 300 K, vil ha maksimal utstråling for bølgelengder rundt 10 μm som er i den infrarøde delen av det elektromagnetiske spekteret og blir absorbert i atmosfæren. Dette er en viktig grunn for drivhuseffekten. Den kosmiske bakgrunnstrålingen har en temperatur i dag på T = 2,73 K som tilsvarer bølglengder omkring λm = 1 mm eller frekvenser rundt 300 GHz.
Stråling og materie[rediger | rediger kilde]

Max Planck ble Kirchhoffs etterfølger ved Universitetet i Berlin i 1892. Et par år senere ble han med på et forskningsprsjekt som skulle avgjøre om det var gasslamper eller elektrisk lys som ga best belysning i byen. I denne sammenhengen innså han nødvendigheten av å formulere en troverdig strålingslov. I 1897 da han var 38 år gammel, annonserte han at hans oppgave framover skulle være å utlede Wiens strålingslov som han var overbevist om var riktig. Den var foreslått året før av Wilhelm Wien.[2] Planck mente at løsningen måtte finnes ved bruk av termodynamikk kombinert med Maxwells ligninger for de elektromagnetiske bølgene strålingen besto av.
Termisk likevekt[rediger | rediger kilde]
Man hadde på den tid ingen god forståelse for hvordan strålingen koblet til materie ved emisjon og absorpsjon. Som en modell kunne man tenke seg at den besto av atomer med ladete partikler i bevegelse som Hendrik Lorentz hadde gjort i 1895 for å forklare hvordan spektrallinjene fra forskjellige stoffer ble påvirket av magnetfelt. Men selve eksistensen av atomer på den tiden var meget kontroversiell. Etter at J.J. Thomson oppdaget elektronet i 1897 ble denne muligheten mer troverdig.
Gustav Kirchhoff hadde vist at sort stråling ville ha de samme egenskaper uansett hva slags materie den var i termisk likevekt med. Planck antok derfor at han kunne modellere materien som bestående av små resonatorer som man i dag ville ha kalt atomer. På samme måte som Hendrik Lorentz antok han at dette var en harmonisk oscillator med en gitt frekvens. Den kunne da koble til stråling med samme frekvens. En elektromagnetisk bølge vil få den til å svinge og energi blir dermed absorbert fra bølgen. Men den samme svingningen vil samtidig medføre at oscillatoren sender ut stråling, og det vil etter hvert kunne etableres en energibalanse. For hver frekvens i strålingen, må det finnes en slik resonator med samme frekvens slik at hele spektret av bølger i strålingen kan komme i termisk likevekt.
Harmonisk oscillator koblet til stråling[rediger | rediger kilde]
Enklest er det å tenke seg en Lorentz-oscillator som kun kan svinge i x-retningen. Da er det bare komponenten Ex cosωt av det elektriske feltet til en bølge med frekvens ω = 2πν som virker på den. Har den oscillerende partikkelen en masse m, elektrisk ladning e og svinger med egenfrekvens ω0, vil den da få en bevegelse gitt ved
som følger fra Newtons andre lov. Frekvensen ω til bølgen antas å være omtrent den samme som egenfrekvensen. På grunn av utstrålingen kommer det på høyresiden av ligningen en ekstra friksjonskraft som kan skrives som γdx/dt. Her er konstanten γ = (e2/4πε0)⋅(2ω2/3mc3) som kan regnes ut i klassisk elektrodynamikk hvor Coulombs konstant 1/4πε0 inngår. Resonatoren blir drevet av det elektriske feltet og oscillerer som x(t) = A cosωt hvor amplituden A = A(ω) nå kan regnes ut. Denne oscillasjonen gir resonatoren energien E = mω02A2/2. Etter å ha brukt at ω ≈ ω0, kan denne skrives som
etter å ha innført Γ = γ/2m som en forenkling av uttrykket. Denne energien har et klart maksimum for ω = ω0 som betyr at den resonerer ved denne frekvensen. Men den mottar også strålingsenergi fra nærliggende frekvenser. Fra et lite frekvensintervall Δω rundt ω0 kan man finne den totale energien ved å integrere over alle frekvensene ω. Skriver man resultatet av dette som E(ω0)Δω, har man derved
hvor E(ω0) er den midlere energien til resonatoren når den befinner seg i termisk likevekt med den sorte strålingen. Denne har en energitetthet uω Δω = uν Δν som er tre ganger ε0Ex2/2 da bidragene fra de to andre, elektriske komponentene er like store for isotropisk stråling. Her er uω er den spektrale energitettheten med hensyn på frekvensen ω = 2πν. Skriver man heretter ω for ω0 og benytter sammenhengen uν = 2π uω, følger det at
hvor det er gjort tydelig at dette gjelder ved en bestemt temperatur. Dette er den fundamentale relasjonen Planck utledet i 1899 mellom strålingtettheten og den midlere energien til en harmonisk oscillator i veggen som den sorte strålingen er i likevekt med. Det er bemerkelsesverdig at detaljerte egenskaper som ladning og masse til denne resonatoren, ikke inngår i resultatet. Problemet med å forstå strålingens egenskaper var dermed blitt overført til å finne midlere energi for en oscillator i termisk likevekt. Det virket enklere og burde kunne løses ved bruk av statistisk fysikk.
Fenomenologisk utledning[rediger | rediger kilde]
Planck var overbevist om at det var en absolutt egenskap at systemets entropi aldri kan avta av seg selv. Han hevdet at dette var like grunnleggende som at et systems energi er konstant. I 1877 hadde Ludwig Boltzmann kommet med en annen tolkning av entropi hvor den er bestemt av den mest sannsynlige tilstanden for systemet. Planck brydde seg lite om dette. Han hadde bestemt seg for at han ville utlede Wiens lov ved å vise at den generelle egenskapene til strålingen kunne begrunnes ut fra at termodynamikkens andre lov er absolutt.
Planck-Wiens strålingslov[rediger | rediger kilde]
Tidlig i 1900 kunne han presentere en utledning som viste at den spektrale energitettheten måtte være på formen[3]
i overensstemmelse med Wiens strålingslov. De to konstantene C og b kunne bestemmes slik at formelen stemte med målinger primært utført av F. Paschen for bølgelengder λ = 1 μm - 4 μm.[4][5] Denne enkle strålingsloven ble nå omtalt som Planck-Wiens formel da den var i overensstemmelse både med teori og eksperiment.
Men i løpet av høsten 1900 ble resultatet av nye målinger kjent. De var utført av Rubens og Kurlbaum[6][7] og bekreftet tidligere observasjoner gjort av Lummer og Pringsheim for bølgelengder opp til 18 μm.[8] Rubens hadde informert Planck om disse nye resultatene før de var blitt bekjentgjort. De var gjort ved lavere frekvenser i området for infrarød stråling som tilsvarer bølgelengder helt opp til 60 μm og observert som Reststrahlen. Her skulle energitettheten ifølge formelen variere som tredje potens av frekvensen, men ble observert å heller variere som kvadratet av den. For en gitt frekvens i dette området varierte den i tillegg proporsjonalt med temperaturen, noe som var i direkte motstrid med hva formelen sa.
Entropien til en Wien-resonator[rediger | rediger kilde]
Fra termodynamikk følger at man alltid må ha sammenhengen (∂S/∂E)V = 1/T mellom entropi S, energi E og temperaturen T. I dette problemet med varmestråligen ble volumet holdt konstant. Planck brukte denne termodynamiske relasjonen til å regne ut entropien til en materiell resonator. Det gjorde han ved å kombinere sin likevektsligning med Wiens formel som ga at energien til resonatoren måtte vœre
som funksjon av temperaturen. Løser man denne ut, finner man 1/T = - (1/bν)log(8πE/Cc3ν) som igjen skal være lik ∂S/∂E. Ved en enkel integrasjon hadde Planck da entropien S(E) til en resonator.
I stedet for å integrere, kan man derivere samme uttrykket med hensyn på energien. Det gir med en gang ∂2S/∂E2 = -1/bνE, noe som Planck fant svært tilfredsstillende da høyresiden her alltid er negativ. Systemet er da garantert å være termodynamisk stabilt med en entropi som ikke kan avta.
Energien til en Planck-resonator[rediger | rediger kilde]
Men de nye måleresultatene hadde vist at alt dette likevel ikke lenger var helt riktig. Planck gikk derfor tilbake til resultatet han hadde funnet for den andrederiverte av entropien som nå bare kunne være riktig for stor verdier av frekvensen ν. Han prøvde å modifisere det slik at han kunne få ny overensstemmelse med dataene samtidig som at kravet ∂2S/∂E2 < 0 alltid var oppfylt. På den måten kom han frem til at
hvor h og k er to ukjente konstanter. Når nå hv >> E, er man tilbake i Wiens tilfelle med b = h/k. Dermed er overensstemmelsen med Wiens lov ved høye frekvenser sikret. Ved så igjen å integrere over energien, fant Planck herav at 1/T = (k/hν) log(1 + hν/E) eller
Innsatt i sin likevektsformel hadde dermed Planck funnet sin nye strålingslov som nå stemte med alle målingene.
Dette revolusjonerende resultatet ble presentert av Planck på et møte i videnskapsselskapet i Berlin den 19. oktober 1900.[9][10] Konstantene h og k inngikk ikke eksplitt i hans utledning slik som her, bare kombinasjonen h/k = b. Men når hν/kT > 1, gjenfinnes Wiens strålingslov med konstanten C = 8πh/c3 slik at de to nye konstantene kunne bestemmes fra målingene. I den motsatte grensen hν/kT < 1 går den over i Rayleigh-Jeans' strålingslov hvor energitettheten til strålingen er proporsjonal med temperaturen som påvist i målingene ved lave frekvenser.
Etter å ha kommet frem til dette resultatet, ble den tidligere Planck-Wiens lov igjen omtalt som kun Wiens strålingslov.
Entropien til en Planck-resonator[rediger | rediger kilde]
Selv om Planck hadde funnet en ny formel som passet til alle måleresulatene, var den likevel ikke mye mer enn en meget god tilpasning til disse. Han visste at han måtte finne en mer solid, teoretisk begrunnelse for det som til en viss grad hadde vært heldig gjetning.
Fremdeles mente han at svaret måtte finnes i entropien S(E) til resonatoren. Ved en omskrivning av hva han hadde funnet tidligere, fulgte at ∂S/∂E = (k/hν) (log(1 + E/hν) - log(E/hν)). Ved å bruke at ∫dx logx = x logx - x kan dette nå integreres direkte med resultatet
Spørsmålet var da redusert til å finne ut hva slags fysikk som skjulte seg bak dette uttrykket for entropien for en harmonisk oscillator.
Planck hadde til dette tidspunkt kun brukt klassisk elektrodynamikk og termodynamikk. Men det var ikke kjent hvordan man fra disse teoriene kunne beregne entropien til et system. Derimot var det kjent at det kunne gjøres ved hjelp av statistisk fysikk etablert spesielt av Ludwig Boltzmann, men Planck var ikke overbevist av riktigheten ved denne metoden. Ifølge termodynamikkens første hovedsetning som formulert av Clausius, kunne entropien til et isolert system aldri avta. Men i den statistiske utledningen til Boltzmann kunne dette skje, selv om det i praksis ville være med en forsvinnende liten sannsynlighet.
Boltzmanns metode[rediger | rediger kilde]
Likevel klarte Planck i løpet av de følgende ukene å utlede entropien for en resonator basert på akkurat Boltzmanns fremgangsmåte for en ideell gass.[11] Han betraktet et antall N resonatorer med samme frekvens og som man kan tenke seg lokalisert på forskjellige steder. Deres samlede energi tenkte han seg oppdelt i et meget stort antall P energielement ε som så kan fordeles blant alle oscillatorene. En slik fordeling vil for eksempel kunne skrives som |εε|ε||εεε|εε......| hvor de forskjellige ocillatorene er adskildt med loddrette streker. I dette eksemplet har den første oscillatoren to element, den andre ett, den tredje ingen, den fjerde tre, og så videre. Den første og siste streken ligger fast i alle fordelingene, mens de andre N - 1 strekene skal fordeles mellom de P energielementene.
Det totale antall slike fordelinger finnes fra standard kombinatorikk og gitt ved binomialkoeffisienten
Ifølge Boltzmann kan nå entropien beregnes fra generelle formelen S = kB logW hvor konstanten kB er Boltzmanns konstant. Antar man at både N og P er mye større enn én, kan man benytte Stirlings formel ved utregningen. Entropien for alle oscillatorene finnes på den måten å være
Men her er nå den totale energien Pε = NE hvor E er den midlere energi til en resonator. Sammenlignet med det tidligere, fenomenologiske resultatet for entropien til en oscillator, ser man her full overensstemmelse når konstanten k = kB og energielementet ε = hν.
Denne teoretiske beregningen ble lagt frem i vitenskapsselskapet i Berlin den 14. desember 1900.[12] Den skulle i årene som fulgte gjøre Planck verdensberømt. Da resonatorene til Planck kun kunne oppta og avgi energi i diskrete energikvant med størrelse ε = hν, representerer hans resultat en avskjed med klassisk fysikk hvor alle slike prosesser skjer på kontinuerlig vis. Den nye fysikken som måtte ligge bak, ble med en gang omtalt som kvantefysikk selv om det skulle gå nesten 25 år til den var fullt forstått med etableringen moderne av kvantemekanikk.
I denne opptellingen av tilstander var det implisitt antatt at alle energielementene var identiske og ikke kunne adskilles fra hverandre. Men siden denne oppdelingen av totalenergien bare var en matematisk antagelse, hadde ikke Planck noen problemer med det. I virkeligheten hadde han håpet å kunne ta grensen ε → 0 på slutten av beregningen slik som Boltzmann hadde gjort for en gass, men det var altså ikke mulig i dette tilfellet.
Einstein og fotoner[rediger | rediger kilde]
På dette stadium tenkte ikke Planck at disse energikvantene skulle være en egenskap ved selve strålingen. Han mente at strålingen var kontinuerlig, men ble absorbert eller emittert i diskrete porsjoner av størrelse ε = hν. Det var Einstein som i de følgende årene viste ved bruk av statistisk fysikk at disse kvantene var en egenskap ved selve strålingen. Han fant at de også kunne tilskrives en bevegelsesmengde p = hv/c slik at de på alle måter oppførte seg som partikler. I dag kalles disse for fotoner og er en grunnleggende del av moderne kvantefeltteori.
Gass av energikvant[rediger | rediger kilde]
Einstein skrev sitt første arbeid om varmestråling i 1905.[13] Vel femten år senere ble dette lagt til grunn for å tildele han Nobelprisen i fysikk. I stedet for å beregne entropien til resonatorene i veggene som omsluttet strålingen slik Planck hadde gjort fem år tidligere, ville Einstein undersøke entropien til selve strålingen. Han tok da utgangspunkt i Wiens strålingslov som beskriver den riktig ved lave intensiteter. Fra den spektrale strålingstettheten uν(T) følger da at temperaturen kan skrives som 1/T = (1/bν)log(Cν3/uν). Betrakter man nå et volum V med strålingen, så inneholder det den totale energien Uν(T) = uν(T)V i det samme spektrale området. Den tilsvarende entropien Sν kan finnes fra den termodynamiske relasjonen (∂Sν/∂Uν)V = 1/T da den gjelder for hver frekvens som finnes i strålingen. Ved her å sette inn for 1/T og utføre den samme integrasjonen ∫dx logx = x logx - x som Planck hadde benyttet tidligere, fant Einstein for strålingsentropien
Hvis nå volumet forandres fra V1 til V2 ved konstant energi, vil entropien til strålingen forandres med
hvor b = h/kB. Sammenlignes dette med entropien til en ideell gass med partikler, ser man at resultatet for strålingen har samme form når Nν = Uν/hν tolkes som antall partikler i en gass med stråling. Hver partikkel er da et energikvant med energi ε = hν. Dette var det matematiske resultatet som overbeviste Einstein om at strålingen kunne beskrives som slike diskrete energikvant. Som en konskvens av denne innsikten viste han i det samme arbeidet at den fotoelektriske effekten måtte ha visse egenskaper som senere ble eksperimentelt verifisert. Dette ga han Nobelprisen i fysikk i 1921.
At strålingen skulle bestå av diskrete energikvant, var selvfølgelig i radikal konflikt med klassisk fysikk og Maxwells ligninger hvor alle fenomen skjer kontinuerlig. Det var også i konflikt med Plancks utledning hvor selve strålingen var antatt å være kontinuerlig, mens det var bare ved kobling til materialet i veggene at energi skulle bli opptatt og avgitt i diskrete porsjoner. Disse konfliktene ville oppta Einstein i årene som kom.[14]
Klassisk harmonisk oscillator[rediger | rediger kilde]
Allerede i 1907 bidro Einstein med en kvanteteoretisk forklaring av egenskapene til materialet i veggene som omsluttet strålingen.[15] Til da hadde man ikke hatt noen god forståelse av atomene som materialet var ment å bestå av. I stedet omtalte man dem som resonatorer, og Planck hadde antatt at de var vanlige, harmoniske oscillatorer. Har en slik oscillator massen m og en kraftkonstant k, så vil dens energi være gitt som E = p2/2m + kq2/2. Den varierer kontinuerlig med utslaget q og impulsen p og svinger med vinkelfrekvensen ω = √(k/m). Fra statistisk fysikk er sannsynligheten for at oscillatoren har energien E ved en temperatur T proporsjonal med Boltzmanns faktor exp(-βE) hvor β = 1/kBT. Den midlere energien er derfor
Her inngår normeringsfaktoren
som ofte kalles for partisjonsfunksjonen. Er den regnet ut, kan den midlere energien beregnes mye enklere som <Eν> = - ∂ log Z/∂β. Denne relasjonen gjelder helt generelt og spiller en sentral rolle i statistisk fysikk.
Når oscillatoren beskrives klassisk, er den beskrevet ved kontinuerlige variable. Både integralet over p og over q i uttrykket for Z er gitt ved det vanlige Gauss-integralet ∫dx exp(-x2) = √π når integrasjonsgrensene er ±∞ som i dette tilfellet. Dette gir at Z = 2π /βω og derfor den midlere oscillatorenergien <Eν> = kBT. Innsatt i Plancks likevektsformel, kom Einstein på denne måten frem til Rayleigh-Jeans' strålingslov.
Partisjonsfunksjonen Z kan også regnes ut på en annen måte som Einstein gjorde bruk av. Definerer man funksjonen
hvor δ(x) er Diracs deltafunksjon, så har man i stedet at Z = ∫ dE ρ(E) exp(-βE). For oscillatoren finner man ρ = 2π /ω som igjen gir Z = 2π /βω.
Kvantisering av harmonisk oscillator[rediger | rediger kilde]

Utfra disse betraktningene visste Einstein nå at det ikke var riktig å beskrive oscillatorene ved klassisk fysikk. Planck hadde fem år tidigere vist at de kun kunne oppta og avgi energi i form av energikvant med størrelse ε = hν med ν = ω/2π. Energien til en oscillator kan derfor bare anta diskrete verdier En = nhν hvor n = 0,1,2,3,.... og til uendelig. Man sier at dens energier er kvantisert. I uttrykket for partisjonsfunksjonen Z kan man ikke lenger integrere over alle verdier, men må i stedet summere opp de diskrete bidragene fra hver av energiene. Det gir
Den midlere energien til oscillatoren er derfor
Einsteins fundamentale resultat for energien til den kvantiserte oscillatoren gir nå direkte Plancks strålingsformel. I grensen hν << kBT gjenfinner man det klassiske resultatet som tilfredsstiller formelen til Rayleigh og Jeans. Den er like mye knyttet til Einsteins navn som var den som virkelig innså dens betydning og derfor kunne generalisere den inn i det kvantemekaniske regimet.
Knapt fem år senere skulle Peter Debye benytte denne beregningen til å gi en mer fullstendig forståelse av egenskapene til Einsteins energikvant i selve strålingen. Da gjaldt ikke resultatet lenger for oscillatorene som ble antatt å beskrive svingningene til molekylene eller atomene i veggene, men derimot for svingningene i det elektromagnetiske strålingsfeltet. På den måtene ble Plancks strålingslov enda mer troverdig da den ikke lenger var avhengig av spesielle antagelser om egenskapene til materialet i veggene.
Det klassiske resultatet <Eν> = kBT er en del av ekvipartisjonsprinsippet som tidligere var benyttet til å beregne den spesifikke varmekapasiteten for forskjellige stoffer og formulert som Dulong-Petits lov. Det var kjent at flere faste stoffer viste avvik fra denne ved lave temperaturer. Dette fikk Einstein i samme arbeid til å foreslå at hans kvantemekaniske resultat for <Eν> kunne benyttes til å beregne varmekapasiteter på en ny måte. Basert på en enkel modell for faste stoffer fant han også mye bedre overensstemmelse med målingene.
Fluktuasjoner i strålingen[rediger | rediger kilde]
Energien E til et system som er i termisk likevekt ved temperaturen T, er ikke helt konstant da det hele tiden utveksler små energimengder med omgivelsene for at temperaturen skal forbli uforandret. Den midlere energien <E> kan beregnes ved bruk av Boltzmanns sannsynlighetsfordeling P(E) = exp(-βE)/Z som allerede brukt for oscillatorene i veggene. På samme måte kan man regne ut den midlere, kvadratiske energien <E2>. Denne viser seg da å ikke være den samme som kvadratet av den midlere energien. Differensen mellom disse to størrelsene er fluktuasjonen av energien. Ved direkte utregning følger at den er gitt som
Einstein var overbevist om at disse relasjonene som følger fra statistisk fysikk, også måtte gjelde for varmestrålingen. Tidlig i 1909 publiserte han nok et viktig arbeid hvor han kom frem til nye, fundamentale egenskaper til strålingen basert på slike statistiske metoder.[16] I et volum V og frekvensintervall Δν har strålingen en midlere energi <E> = VuνΔν hvor den spektrale energitettheten er gitt ved Plancks lov. Ved bruk av den generelle formelen for fluktuasjonen, fant han da ved direkte derivasjon resultatet
for fluktuasjonen av denne energien. Den første termen ville ha kommet frem hvis man hadde brukt Wiens strålingslov for energitettheten. Og det var denne som Einstein i 1905 hadde vist førte til at strålingen kunne beskrives som en gass av partikler eller energikvant. På samme måte ville det siste leddet ha kommet frem hvis man hadde brukt Rayleigh-Jeans' strålingslov som følger fra bølgeteori. Med denne beregningen kunne derfor Einstein konkludere at Plancks formel måtte bety at strålingen bestod av bestanddeler som samtidig måtte være både partikler og bølger. Han hadde på den måten åpnet opp en ny dør til kvantemekanikkens verden hvor partikler har bølgeegenskaper. Det tok likevel nesten femten år til før dette ble helt forstått og matematisk formulert.
Fotonet har impuls[rediger | rediger kilde]
Formelen som Einstein hadde funnet for energifluktuasjonene, utledet han i samme arbeidet også på en annen måte ved å betrakte hvordan hastigheten til et speil plassert i strålingen ville fluktuere. En tolkning av resultatet var at energikvantene også hadde en rettet bevegelsesmengde eller impuls. På et stort fysikkmøte i Salzburg om høsten 1909, hvor han også for første gang ga en offentlig presentasjon av sin spesielle relativitetsteori, diskuterte han også egenskapene til varmestråling og denne egenskapen ved Plancks energikvant.[17] Dette var igjen i motsetning til klassisk fysikk hvor utsendelse av stråling fra et materielt punkt skjer i form av kulebølger med samme intensitet i alle retninger. Et utsendt energikvant syntes derimot å måtte ha en bevegelse rettet i en bestemt, men vilkårlig retning. Fra hans spesielle relativitetsteori følger at denne impulsen må være hν/c for et kvant med energi hν og som beveger seg med lyshastigheten c. I stedet for at lys ble emittert som en kulebølge likt i alle retninger, må det tilsvarende kvantet bevege seg i en bestemt retning - som en nål.
På tross av disse argumentene fant Einstein liten aksept for sin beskrivelse av strålingen som bestående av kvanter. Det viktigste motargumentet var at en slik partikkelteori ikke kunne gi noen forklaring av interferens som er så karakteristisk for lys og annen elektromagnetisk stråling. Likevel forsatte Einstein i de følgende årene med å overbevise seg selv og andre om at hans bilde av strålingens egenskaper var riktig.
I 1917 presenterte han et nytt arbeide hvor han betraktet et enkelt atom i et strålingsfelt.[18] Da var Bohrs atommodell etablert, og man hadde derfor en mye mer realistisk forståelse av dets egenskaper. For at strålingen skal være i termisk likevekt, må atomet emittere og absorbere energikvant på en bestemt måte som tilsvarer at den har energitetthet som er gitt ved akkurat Plancks strålingslov. Einstein mente senere at dette var for han den mest tilfredsstillende utledningen som kunne gis av denne formelen. I tillegg kom han her frem til sine berømte strålingskoeffisienter som gir sannsynlighetene for atomet skal emittere og absorbere lys. Denne formuleringen la grunnlaget for virkningen av laseren. Fra samme betraktning fulgte også at energikvantene må ha en rettet impuls som gir atomet en nødvendig rekyl som inngår i betingelsene for likevekt. Fem år senere ble fotonets energi hν og impuls hν/c eksperimentelt påvist i Compton-effekten. Siden er fotonet kjent som en partikkel. Men dette er ingen klassisk partikkel, men en kvantepartikkel som følger Bose-Einstein-statistikk.
Kvantisering av strålingen[rediger | rediger kilde]
Einsteins utledning av strålingstettheten var basert på Plancks opprinnelige formel som uttrykte den ved den midlere energien for de materielle oscillatorene som til da var antatt å beskrive atomene i veggene som omsluttet strålingen. De fleste var klar over at en slik oscillatormodell for et atom ikke kunne være riktig. Derfor var det viktig å finne en utledning som var uavhengig av denne antagelsen.
Elektromagnetiske moder[rediger | rediger kilde]
Dette ble gjort av den nederlandske fysikeren Peter Debye i 1910.[19] Han tok utgangspunkt i selve strålingsfeltet på samme måte som John William Strutt (lord Rayleigh) hadde gjort ved utledningen av sin strålingslov. Det elektriske feltet E(x,y,z,t) til strålingen må oppfylle Gauss' lov ∇⋅E = 0 samtidig som det må stå normalt på veggene til volumet V som inneslutter strålingen. Er dette en kube med sidekant L slik at V= L3, betyr det at for eksempel at komponenten Ez må være null på de fire sidene x = 0,L og y = 0,L til kuben som er parallelle med z-aksen. Samtidig kan man ut fra symmetri anta at denne komponenten av feltet har samme verdi på sidene z = 0,L. Derfor vil den tillatte formen av denne funksjonen være
hvor de hele tallene n = (nx, ny, nz) karakteriserer hver slik løsning eller mode og E0z(t) er en ennå ubestemt funksjon. De to andre komponentene Ex og Ey vil kunne skrives på tilsvarende måte. Det følger da direkte at divergensen ∇⋅E = 0 hvis alle tre komponentene inneholder de samme modetallene og n⋅E0 = 0 hvor vektoren E0(t) = (E0x, E0y, E0z). Den står derfor normalt på vektoren n og har derfor kun to uavhengige retninger i hver mode. Disse tilsvarer de to polarisasjonsretningene til et foton.
Feltoscillatorer[rediger | rediger kilde]
Det variable elektriske feltet i strålingen er koblet sammen med det magnetiske feltet gjennom Maxwells ligninger. Som en direkte konsekvens må hver komponent oppfylle den elektromagnetiske bølgeligningen
hvor c er lyshastigheten og ∇2 er Laplace-operatoren. Benytter man her den funne formen til hver av komponentene, reduserer denne ligningen seg til
ved å innføre størrelsen ω2 = (πc/L)2n⋅n. Denne ligningen er nå ikke noe annet enn bevegelsesligningen for en harmonisk oscillator med vinkelfrekvense ω. Hver mode av det elektromagnetiske feltet varierer derfor med tiden akkurat som de harmoniske svingningene til en oscillator.
Det er viktig å være klar over at disse feltoscillatorene er noe ganske annet enn de tidligere, materielle oscillatorene som man antok fantes i veggene til beholderen. Disse er mer abstrakte, men følger direkte fra de fundamentale ligningene til Maxwell. I motsetning til de materielle oscillatorene som var lokaliserte i veggene, kan man ikke si hvor i rommet disse feltoscillatorene befinner seg. Femten år senere vil dette bli forstått som et uttrykk for Heisenbergs uskarphetsrelasjon.
Energien til en strålingsoscillator er nå gitt ved samme uttrykk som Einstein hadde funnet for en materiell oscillator. Hver mode av feltet har en energi som er et helt antall multiplisert med hν hvor ν = ω/2π er frekvensen til oscillatoren. Det gir den samme, midlere energien ved temperaturen T. Antall slike feltoscillatorer per volumenehet var tidligere funnet ved utledningen av Rayleigh-Jeans' strålingslov å være 8πν2/c3. På den måten fant Debye resultatet
for den termiske energitettheten til strålingen. Og dette er akkurat Plancks lov. Den er beregnet uten usikre antagelser om egenskapene til materialet i veggene som omslutter strålingen, noe som Debye la vekt på ved sin nye utledning.
Denne beregningen av strålingsenergien er den som normalt i dag blir brukt i undervisning og presentert i lærebøker. Den er tett opp til den mer moderne utledningen ved bruk av kvantefeltteori som ligger bak Bose-Einstein statistikk. Det er først en slik fullstendig beregning som også tillater å finne Einsteins fluktuasjonsformel.
Referanser[rediger | rediger kilde]
- ^ O. Lummer und E. Pringsheim, Verhandlungen der Deutschen Physikalischen Gesellschaft 2, 176 (1900).
- ^ W. Wien, Ueber die Energievertheilung im Emissionsspectrum eines schwarzen Körpers, Annalen der Physik 294 (8), 662–669 (1896). PDF.
- ^ M. Planck, Entropie und Temperatur strahlender Wärme, Annalen der Physik 1(4), 719-737 (1900). PDF.
- ^ F. Paschen, Annalen der Physik und Chemie 58, 455-492 (1896); 60, 663-723 (1897).
- ^ F. Paschen, Sitzungsberichte der Akademie der Wissenschaften zu Berlin, 405, 959 (1899).
- ^ H. Rubens und F. Kurlbaum, "Über die Emission langwelliger Wärmestrahlen durch den schwarzen Körper bei verschiedenen Temperaturen, Sitzungsberichte der Akademie der Wissenschaften zu Berlin, 929-941 (1900). PDF
- ^ H. Rubens und F. Kurlbaum, Anwendung der Methode der Reststrahlen zur Prüfung des Strahlungsgesetzes, Annalen der Physik 309 (4), 649-666 (1901). PDF
- ^ O. Lummer und E. Pringsheim, Verhandlungen der Deutschen Physikalischen Gesellschaft 1, 23, 215 (1899); 2, 163 (1900).
- ^ M. Planck, Zur Theorie des Gesetzes der Energieverteilung im Normalspectrum, Sitzungsberichte der Akademie der Wissenschaften zu Berlin, 237-245 (1900). «Arkivert kopi» (PDF). Arkivert fra originalen (PDF) 7. august 2015. Besøkt 6. mai 2014.
- ^ M. Planck, Über eine Verbesserung der Wienschen Spektralgleichung, Verhandlungen der Deutschen Physikalischen Gesellschaft 2, 202–204 (1900). PDF Arkivert 7. mars 2016 hos Wayback Machine..
- ^ L. Boltzmann, Über die Beziehung zwischen dem zweiten Hauptsatz der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht, Wiener Berichte 76, 373–435 (1877).
- ^ M. Planck, Über das Gesetz der Energieverteilung im Normalspektrum, Annalen der Physik 309 (4), 553-563 (1901). PDF.
- ^ A. Einstein, Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt, Annalen der Physik 17, 132-148 (1905). PDF
- ^ A. Einstein, Zur Theorie der Lichterzeugung und Lichtabsorption, Annalen der Physik, 20, 199-206 (1906). PDF
- ^ A. Einstein, Die Planckshe Theorie der Strahlung und die Theorie der spezifischen Wärme, Annalen der Physik, 22, 180-190 (1907). PDF
- ^ A. Einstein, Zum gegenwärtigen Stand des Strahlungsproblems, Phys. Zeitschrift 10, 185 - 193 (1909).
- ^ A. Einstein, Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung, Phys. Zeitschrift 10, 817–825 (1909). Engelsk oversettelse, Wikisource.
- ^ A. Einstein, Zur Quantentheorie der Strahlung, Phys. Zeitschrift 18, 121 - 128 (1917).
- ^ P. Debye, Der Wahrscheinlichkeitsbegriff in der Theorie der Strahlung, Annalen der Physik 33, 1427-1434 (1910).
Litteratur[rediger | rediger kilde]
- M. Planck, The Theory of Heat Radiation, Dover Publications, New York (2003). ISBN 0-486-66811-8.
- F. Reif, Fundamentals of Statistical and Thermal Physics, McGraw-Hill Kogakusha Ltd., Tokyo (1965).
- M. Longair, Theoretical Concepts in Physics, Cambridge University Press, England (2003). ISBN 978-0-521-82126-1.







![{\displaystyle {8\pi hc \over \lambda ^{6}}\left[{xe^{x} \over (e^{x}-1)^{2}}-{5 \over e^{x}-1}\right]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26388533d15d9ffdc52ad391e435524e89bfb7e6)









![{\displaystyle S(E)=k\left[(1+E/h\nu )\log(1+E/h\nu )-(E/h\nu )\log(E/h\nu )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a770ae2dcc6d98c915a706bcf60ace6ec00eff7)

![{\displaystyle S_{N}=Nk_{B}\left[(1+P/N)\log(1+P/N)-(P/N)\log(P/N\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1e00001cce0bbef06e4bd4dc75bd086c9599627)











