Massesentrum
Massefellespunktet (også kalt tyngdepunktet) til et system med partikler er et spesifikt punkt hvor systemet i mange tilfeller oppfører seg som om systemets masse var konsentrert i ett punkt. Massefellespunktet gjelder bare for partiklene som systemet består av. I tilfellet av et stivt legeme, er massefellespunktet et fast punkt i henhold til legemet, men ikke nødvendigvis i kontakt med legemet. For en tilfeldig fordeling av masser vil massefellespunktet kunne være et punkt i rommet som muligens ikke korresponderer til massen hver for seg. I sammenheng med et helt uniformt gravitasjonsfelt, blir massefellespunktet ofte kalt tyngdepunktet, det vil si det punktet hvor det sies tyngdekraften påvirker legemet.
Massefellespunktet stemmer ikke alltid overens med legemets geometriske sentrum. Dette blir utnyttet blant annet av ingeniører som prøver å designe biler med så lavt tyngdepunkt som mulig og høydehoppere som bøyer deres kropp på en slik måte at kroppen overstiger stangen samtidig som deres massesentrum ikke gjør det.
Definisjon[rediger | rediger kilde]
Massesenteret av et system av partikler er definert som gjennomsnittet av deres posisjoner, , vektet på deres masser, :
For en kontinuerlig fordeling av massetetthet og total masse , blir summen et integral:
Dersom et legemes tetthet er uniform blir massesentrumet det samme som det geometriske sentrum.
Eksempler[rediger | rediger kilde]
- Massesentrum til to partikler ligger på den korteste linjen som binder de individuelle partiklenes massesentrum. Massesentrumet er nærmest den partikkelen med den største massen.
- Massesentrum til en ring med jevnt fordelt masse er i midten av ringen (i luften).
- Massesentrum til et rektangel med jevnt fordelt masse er krysningspunktet til de to diagonalene.
Historie[rediger | rediger kilde]
Konseptet av et massesentrum ble først introdusert av den greske matematikeren, fysikeren og ingeniøren Arkimedes. Arkimedes viste at dreiemomentet til en stang var det samme om vekter på stangen var fordelt eller om dem var samlet på et punkt massesenteret. I forsøk med flytende masser viste han at orienteringen til den flytende massen er den samme som gjør deres tyngdepunkt lavest mulig. Han utviklet matematiske teknikker for å finne massesentrum for objekter med jevnt fordelt masse ved hjelp av forskjellige veldefinerte former. I middelalderen ble teoriene om massesentrum videre utviklet av Abu Rayhan Biruni, al-Razi (Latinsk navn «Rhazes»), Omar Khayyám og al-Khazini.[1]
Barysentriske koordinater[rediger | rediger kilde]
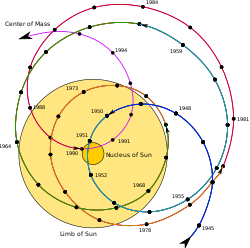
Innen astronomi er barysentriske koordinater ikke-roterende koordinater med opprinnelse i et massefellespunkt for to eller flere himmellegemer.
Barysenteret (eller barysentret; fra gresk: βαρύκεντρον) er det punktet mellom to objekter for de balanserer hverandre. For eksempel er det sentrum av masse der to eller flere himmellegemer går i bane rundt hverandre. Når en naturlig satellitt går i bane rundt en planet, eller en planet går i bane rundt en stjerne, går begge legemene i realiteten i bane rundt et punkt som ligger utenfor sentrum av det primære legemet. For eksempel er ikke sentrum av månens bane rundt jorden i sentrum av jorden, men et punkt på en linje mellom sentrum av jorden og månen, omtrent 1 710 km under jordoverflaten hvor deres respektive masser er i balanse. Dette er det punktet hvis jorden og månen går i bane rundt når de går rundt solen.








