Gravitasjonspotensial

Gravitasjonspotensialet rundt en kuleformet masse er negativt og har et minimum i massens sentrum.

Gravitasjonspotensialet på et sted angir i klassisk fysikk den potensielle energien en masse på samme sted har i nærvær av andre masser på grunn av deres gjensidige gravitasjonskrefter. Gradienten av potensialet gir gravitasjonsfeltet på samme sted og dermed den totale kraften som virker på massen.

Da Newtons gravitasjonslov har samme matematiske form som Coulombs lov for elektriske krefter, spiller gravitasjonspotensialet samme rolle som det elektriske potensialet i elektrostatikken. Men i motsetning til dette, er ikke gravitasjonspotensialet forenlig med den spesielle relativitetsteorien. I stedet lyktes det Einstein å vise at det erstattes med den metriske tensoren i den generelle relativitetsteorien. Den beskriver de geometriske egenskapene til tidrommet som blir krummet på grunn av energi og masse.

Definisjon

Ifølge Newtons gravitasjonslov er kraften F som virker på en liten masse m som befinner seg i en avstand r fra en kuleformet masse M, gitt som

$F={GmM \over r^{2}}$

hvor G er gravitasjonskonstanten. Da kraften er tiltrekkende, må det utføres et arbeid for å flytte m fra avstanden r ut til uendelig hvor kraften er redusert til null. Dette arbeidet

$W=\int _{r}^{\infty }Fdr=-GmM\left({1 \over \infty }-{1 \over r}\right)={GmM \over r}$

er positivt og går med til å overvinne den potensielle energien U massen hadde i sin opprinnelige posisjon. Denne energien er derfor negativ og kan skrives som U = m Φ hvor

$\Phi =-{GM \over r}$

er definert å være gravitasjonspotensialet i avstand r  fra den sfæriske massen M. Det er derfor automatisk lik null når avstanden blir uendelig stor. Istedet kunne potensialet ta en eller annen konstant verdi. Det er mulig da kunne differenser i potensiell energi har fysisk betydning.

Jordens gravitasjonspotensial

Med stor nøyaktighet er Jorden en kuleformet masse. Har den radius R, er gravitasjonspotensialet på overflaten lik med Φ₀ = - GM/R. I en høyde h over jordoverflaten er det øket til Φ = - GM/(R + h). Så lenge som h << R, kan dette forenkles til Φ = Φ₀ + gh  hvor g = GM/R² = 9.82 m/s²  er tyngdeakselerasjonen på Jordens overflate. Da Φ₀ her kan betraktes som en konstant, er det vanlig å si at gravitasjonspotensialet ved Jordens overflate ganske enkelt er Φ = gh.

En masse m som slippes løs i høyden h, vil begynne å falle nedover med økende hastighet v. Etter å ha falt ned til overflaten h = 0, er den potensielle energien m Φ gått over til kinetisk energi mv²/2. Massen har da fått en hastighet

$v={\sqrt {2gh}}$

som følger fra energibevarelse. Hastigheten er uavhengig av størrelsen m, noe som er grunnlaget for ekvivalensprinsippet som ble først formulert av Galileo Galilei.

Inni Jorden kan man bruke Newtons skallteorem til å finne gravitasjonspotensialet. Det sier at gravitasjonsfeltet i en viss avstand r  fra sentrum til en sfærisk symmetrisk massefordeling er bestemt alene av massen innenfor et kuleskall med radius r. For r < R er derfor tyngdeakselerasjonen g(r) = gr/R når man antar at massetettheten ρ er konstant. Gravitasjonspotensialet i dette området er derfor gitt ved

$\Phi -\Phi _{0}=\int _{R}^{r}g(r)dr={g \over 2R}(r^{2}-R^{2})$

Siden man har at Φ₀ = - gR, kan man skrive resultatet som

$\Phi ={g \over 2R}(r^{2}-3R^{2})\qquad r\leq R$

Det har verdien -3gR/2  i Jordens sentrum og øker derfra med kvadratet av radius. Ved Jordens overflate går det kontinuerlig over i potensialet Φ = - GM/r  som gjelder i området utenfor der r > R.

Unnslipningshastighet

Bevegelsen til prosjektilet er avhengig av utskytningshastigheten. Mens A og B er deler av ellipsebaner med lav hastighet, viser C og D bundne baner omkring Jorden. I tilfellet E forlater prosjektilet Jorden langs en hyperbelbane.

Skytes en ball ut med en kanon eller sendes en rakett opp fra Jorden og man ser bort fra luftmotstanden, vil den følge en Kepler-bane som er et kjeglesnitt med Jordens sentrum som et brennpunkt. Avhengig av størrelsen v₀  og retningen til hastigheten i utgangspunktet, vil prosjektilet falle ned på Jorden igjen, gå inn i en lukket bane omkring Jorden eller forlate den fullstendig. I dette siste tilfellet vil den til slutt bevege seg så langt bort at gravitasjonspotensialet blir null. Den har da kun en kinetisk energi som alltid er positiv. Bevarelse av den totale energien til prosjektilet med masse m må da oppfylle

${1 \over 2}mv_{0}^{2}+m\Phi _{0}\geq 0$

hvor Φ₀ = - gR igjen er gravitasjonspotensialet på utskytningsstedet. For at prosjektilet skal unnslippe fra Jorden må derfor

$v_{0}\geq v_{\infty }={\sqrt {2gR}}$

hvor v_∞  er unnslipningshastigheten. Settes her inn R = 6371 km, finner man v_∞ = 11.2 km/s.

Hvis hastigheten til prosjektilet er mindre enn denne kritiske hastigheten, vil det gå inn i en ellipsebane med negativ energi. Skriver man denne som E = - GMm/2a hvor parameteren a > 0 for en slik bunden bevegelse, vil hastigheten v til prosjektilet og dets avstand til Jorden r alltid være forbundet ved ligningen

$v^{2}=GM\left({2 \over r}-{1 \over a}\right)$

som igjen uttrykker bevarelse av dets totale energi. Parameteren a angir lengden til den store halvaksen til ellipsen. Denne sammenhengen kalles noen ganger for vis-viva-ligningen fra den gang vis-viva var navnet for kinetisk energi. Ved å la parameteren a være negativ, gjelder den også for ubundne baner som har form av hyperbler. Det kritiske tilfellet hvor energien er nøyaktig lik null slik at a = ∞, tilsvarer en parabelbane der prosjektilet ender opp med null hastighet uendelig langt bort.

Tidekrefter

En masse m i et generelt gravitasjonspotensial Φ vil påvirkes av gravitasjonsfeltet g = - ∇ Φ som gir opphav til kraften F = m g. Da potensialet vil variere med stedet, vil denne gravitasjonskraften i allminnelighet være litt forskjellig i to nærliggende posisjoner. Denne differansen kalles en tidekraft og gir opphav til tidevann på Jorden og lignende fenomen på andre planeter.

Hvis man betrakter en partikkel i avstand R fra en sentral masse M, befinner den seg i potensialet Φ = - GM/R. Velger man en z-akse i radiell retning, vil partikkelen dermed være utsatt for feltet g_z(0) = - GM/R². En annen partikkel litt lenger ut i avstand R + z, vil tilsvarende befinne seg i feltet g_z(z) = - GM/(R + z )². Differansen mellom disse to

$\Delta g_{z}=g_{z}(z)-g_{z}(0)=2z{GM \over R^{3}}$

når man antar at z << R. Da denne er positiv, betyr det at partikler i disse to posisjonene vil bli drevet bort fra hverandre.

Tidevann på Jorden skyldes at gravitasjons-kraften fra Månen er sterkere på siden som vender mot den og svakere på siden som vender bort fra den, enn i Jordens sentrum.

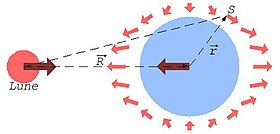
Da feltet g er rettet mot sentrum til massen M, vil det ha samme størrelse, men litt forskjellig retning i et punkt i avstand x vinkelrett på z-aksen sammenlignet med feltet i origo. Denne differansen er gitt ved x-komponenten av det radielle feltet og er dermed

$\Delta g_{x}=-x{GM \over R^{3}}$

Da den er negativ, vil partikler i disse to posisjonene transvers til forbindelseslinjen mellom massene, ble trukket mot hverandre. Det samme gjelder for to posisjoner separert på samme måte i y-retning.

Disse tre differansene i gravitasjonsfeltet kan skrives som den negative gradienten Δg = - ∇ Ψ av potensialet

$\Psi (\mathbf {r} )=-{GM \over R^{3}}\left(z^{2}-{1 \over 2}x^{2}-{1 \over 2}y^{2}\right)=-{GMr^{2} \over 2R^{3}}\left(3\cos ^{2}\theta -1\right)$

etter å ha innført sfæriske koordinater x = r sinθ cosφ, y = r sinθ sinφ og z = r cosθ. Vinkelavhengigheten er gitt ved det andre Legendre-polynomet P₂(cos θ) som er karakteristisk for et kvadrupolmoment.

På Jorden skyldes disse tidekreftene påvirkningen fra Månen og Solen. De virker på partiklene i havvannet som holdes på plass av Jordens eget gravitasjonsfelt. Men kombinasjonen av disse to effektene betyr at havnivået ikke er helt konstant, men får ulik høyde på forskjellige steder. Partikler på forbindelseslinjen til den eksterne massen med θ = 0^° eller 180^° blir trukket bort fra Jorden, mens partikler normalt til denne retningen med θ = 90^° og eller 270^° blir trukket inn mot sentrum. Den resulterende høydeforskjellen vil flytte seg med jordrotasjonen og kalles tidevann. Den vil ha et maksimum to ganger i døgnet.

Kontinuerlig massefordeling

Potensialet i punktet r får bidrag fra alle mikroskopiske masser dm'  i punkt r'  innen den kontinuerlige massefordelingen.

Med mange masser m_i  i posisjoner r_i er gravitasjonspotensialet i et punkt r gitt som summen av potensialene fra hver enkelt masse,

$\Phi (\mathbf {r} )=-\sum _{i}{Gm_{i} \over |\mathbf {r} -\mathbf {r} _{i}|}$

Når alle disse enkeltmassene utgjør en kontinuerlig massefordeling med tetthet ρ, kan hver av dem erstattes med den infinitesemale massen dm'  = ρ(r')dV'  i volumelementet dV'  som befinner seg i r'. Summen over enkeltmassene kan nå erstattes av en integrasjon slik at potensialet i et vilkårlig punkt er gitt som

$\Phi (\mathbf {r} )=-\int \!d^{3}x'{G\rho (\mathbf {r'} ) \over |\mathbf {r} -\mathbf {r'} |}$

Denne generelle formelen er også gyldig når punktet r ligger inni den kontinuerlige massefordelingen.

En mikroskopisk versjon av samme ligning kan finnes ved å bruke den fundamentale egenskapen

$\nabla ^{2}{1 \over |\mathbf {r} -\mathbf {r'} |}=-4\pi \delta (\mathbf {r} -\mathbf {r'} )$

til Laplace-operatoren ∇² hvor på høyre side Diracs deltafunksjon inngår. Gravitasjonspotensialet i det generelle tilfellet tilfredsstiller derfor Poissons ligning

$\nabla ^{2}\Phi (\mathbf {r} )=4\pi G\rho (\mathbf {r} )$

som er Newtons gravitasjonslov på differensiell form. Det er på denne formen den følger fra Einsteins feltligning i generell relativitetsteori når denne anvendes i Newtonsk mekanikk.

Massiv kule

Gravitasjonsfeltet både inni r < R  og utenfor r' > R  en sfærisk symmetrisk massefordeling kan beregnes eksakt og er overalt rettet inn mot kules sentrum.

Gravitasjonspotensialet innenfor og utenfor en massive kule med konstant tetthet ρ kan lett finnes fra Newtons skallteorem. Det er ekvivalent med å løse differensialligningen for gravitasjonspotensialet for denne sfæriske geometrien hvor Laplace-operatoren må uttrykkes i kulekoordinater. Ligningen som må løses, er derfor

${1 \over r^{2}}{\partial \over \partial r}{\Big (}r^{2}{\partial \Phi \over \partial r}{\Big )}=4\pi G\rho$

Utenfor kulen hvor massetettheten ρ = 0, finner man herav at r²(∂Φ/∂r) må være lik en konstant. Kaller man den for GM, varierer derved potensialet utenfor kulen som Φ = - GM/r. Det tilsvarer et potensial fra en punktmasse M i kulens sentrum som er innholdet av skallteoremet i dette tilfellet.

På samme måte finner man at inni kulen i en avstand r  fra dens sentrum at differensialligningen etter en integrasjon forenkles til ∂Φ/∂r = (4π G/3)ρr. Tettheten er her gitt ved den totale massen som ρ = M/(4πR³/3). Gravitasjonspotensialet i dette området er derfor

$\Phi (r)={2 \over 3}\pi \rho Gr^{2}+\Phi _{c}$

hvor integrasjonskonstanten Φ_c må bestemmes ut fra kravet at potensialet nær overflaten av kulen skal gå kontinuerlig over til verdien Φ(r = R) = - GM/R like utenfor denne. Det gir Φ_c = - 2πρGR² slik at

$\Phi (r)={\frac {2}{3}}\pi \rho G(r^{2}-3R^{2}),\qquad r\leq R,$

i overenstemmelse med hva som tidligere ble funnet fra Newtons skallteorem.

Kosmologisk konstant

Poissons ligning for gravitasjonspotensialet er en differensiell formulering av Newtons gravitasjonslov. Men etter Einsteins generelle relativitetsteori som inneholder en kosmologisk konstant Λ, vet man at denne vil bli modifisert i den newtonske grensen. Den tilsvarende differensialigningen for gravitasjonspotensialet tar da formen

$\nabla ^{2}\Phi (\mathbf {r} )+\Lambda c^{2}=4\pi G\rho (\mathbf {r} )$

hvor c er lyshastigheten. Det betyr at det vil overalt finnes en ekstra tyngdekraft som ikke skyldes tilstedeværelse av masse. Setter man ρ = 0, finnes det tilsvarende potensialet ved integrasjon å være

$\Phi (r)=-{1 \over 6}\Lambda c^{2}{\Big (}x^{2}+y^{2}+z^{2}{\Big )}=-{1 \over 6}\Lambda c^{2}r^{2}$

Den kosmologiske konstanten skaper derfor et gravitasjonsfelt g = - ∇ Φ = (1/3)Λc² r. Når den er positiv, er dette rettet radielt utover og skyver alle masser i denne retning.

Ingen slik frastøtende kraft er blitt påvist ved astronomiske observasjoner innen vårt Solsystem eller innen Melkeveien. Men målinger over kosmologiske avstander har vist at en slik effekt er tilstede. Om denne skyldes Einsteins kosmologiske konstant, en mystisk vakuumenergi eller ny fysikk, er ennå ikke klart.