Dodekaeder

Dodekaeder
		(animasjon)
Type		Platonsk legeme
Dualt polyeder		Ikosaeder
Størrelser
Sider		12 pentagoner
Kanter		30
Hjørner		20
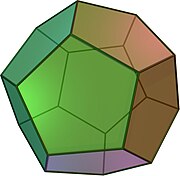
Sidefordeling		5.5.5

Et dodekaeder brettet ut over en todimensjonal flate

En D12-terning er formet som en dodekaeder.

Et dodekaeder er et polyeder med tolv sideflater, men vanligvis menes et regulært dodekaeder: et platonsk legeme satt sammen av tolv like, regulære pentagonale sideflater.

Areal og volum

Overflatearealet A og volumet V av et regulært dodekaeder med kantlengde a er:

$A = 3\sqrt{25+10\sqrt{5}} a^2 \approx 20.645728807a^2$

$V = \frac{1}{4} (15+7\sqrt{5}) a^3 \approx 7.6631189606a^3$

Radius

Hvis et regulært oktaeder med kantlengde a, er radius til en omskrevet kule (en som akkurat fyller ut hele figuren):

$r_u = \frac{a}{4} \left(\sqrt{15} +\sqrt{3}\right) \approx 1.401258538 \cdot a$

Radiusen av en innskrevet kule (en som fyller ut akkurat så mye den kan inne i den) er:

$r_i = \frac{a}{20} \sqrt{250 +110\sqrt{5}} \approx 1.113516364 \cdot a$

Midtradiusen, hvor sideflaten berører midten av alle kantene, er:

$r_m = \frac{a}{4} \left(3 +\sqrt{5}\right) \approx 1.309016994 \cdot a$

Dette kan også bli beskrevet som:

$r_u = \frac{\sqrt{3}}{2} \phi \, a$

$r_i = \frac{\phi^2}{2 \sqrt{3-\phi}} \, a \,\!$

$r_m = \frac{\phi^2}{2} a$

hvor $\phi \,\!$ er det gylne snitt.

Nært dodekaeder

• 

  Avstumpet dodekaeder

• 

  Sløvt dodekaeder

Avstumpingssekvens

• 

  Dodekaeder

• 

  Avstumpet dodekaeder

• 

  Ikosidodekaeder

• 

  Avstumpet ikosaeder

• 

  Ikosaeder

Se også

• Pentagon
• Polyeder
• Platonsk legeme